Jonghyun Ho
코스피 지수의 선형 회귀 분석
코스피 지수 이동평균선 에서 코스피 지수의 이동 방향에 대해 확인할 수 있었다.
이번에는 선형 회귀 분석을 통해 긴 시간의 흐름 동안 전체적인 방향이 어느 곳을 향하고 있는지 분석해 보고자 한다.
선형 회귀
통계학에서 선형 회귀는 설명 변수(explanatory variable) x와 응답 변수(response variable) y 사이의 관계를 선형적으로 모델링하는 것을 말한다.
$y = ax + b$ 의 그래프에서 a 는 기울기, b는 절편으로 직선을 표현할 수 있는데, 설명 변수와 응답 변수의 샘플들을 통해 직선의 기울기와 절편을 파악해내는 것이 목적이다.

선형 회귀에는 하나의 설명 변수를 사용하는 단변량 선형 회귀 (Univariate linear regression)와 여러 개의 설명 변수를 사용하는 다변량 선형 회귀 (Multivariate Linear Regression)가 있다.
여러 가지 변수를 고려하여 지수를 예측할 수도 있겠지만, 우선은 시간의 흐름에 따른 코스피 지수의 변화를 단변량 선형 회귀 (Univariate linear regression)로 확인해보고자 한다.
참고 : Linear Regression
코스피 지수 읽기
최근 1년 동안의 코스피 지수를 구한다.
>>> import numpy as np
>>> import pandas as pd
>>> import matplotlib.pyplot as plt
>>> import yfinance as yf
>>> code = '^KS11' # KOSPI Composite Index
>>> kospi = yf.Ticker(code)
>>> kospi = kospi.history(period='1y')
>>> kospi = kospi[['Close']]
>>> print(kospi)
Open High Low ... Volume Dividends Stock Splits
Date ...
2017-04-17 2140.87 2150.70 2138.70 ... 259300 0 0
2017-04-18 2155.36 2155.36 2139.31 ... 291400 0 0
2017-04-19 2144.98 2148.03 2133.82 ... 344200 0 0
2017-04-20 2138.19 2150.43 2134.05 ... 268300 0 0
2017-04-21 2161.24 2169.46 2156.64 ... 281500 0 0
... ... ... ... ... ... ... ...
2020-04-10 1835.76 1861.10 1824.43 ... 992500 0 0
2020-04-13 1853.30 1853.30 1825.76 ... 1017800 0 0
2020-04-14 1846.41 1864.46 1837.17 ... 886800 0 0
2020-04-16 1857.07 1857.07 1857.07 ... 0 0 0
2020-04-17 1893.31 1926.02 1893.19 ... 1667459 0 0
[727 rows x 7 columns]
학습 샘플 데이터 입력
선형 회귀를 계산하기 위한 설명 변수(explanatory variable) x와 응답 변수(response variable) y의 값을 입력한다.
x는 시간의 흐름, y는 코스피 지수를 의미하고, 기계 학습 알고리즘의 입력 형태를 맞추기 위해 x는 1 * N 행렬에서 N * 1행렬로 변환하였다.
>>> sample_size = len(kospi.Close.index)
>>> X = np.arange(sample_size).reshape(-1, 1)
>>> y = kospi.Close.values
>>> dates = kospi.Close.index
>>> plt.plot(dates[X].flatten(), y)
>>> plt.grid()
>>> plt.show()
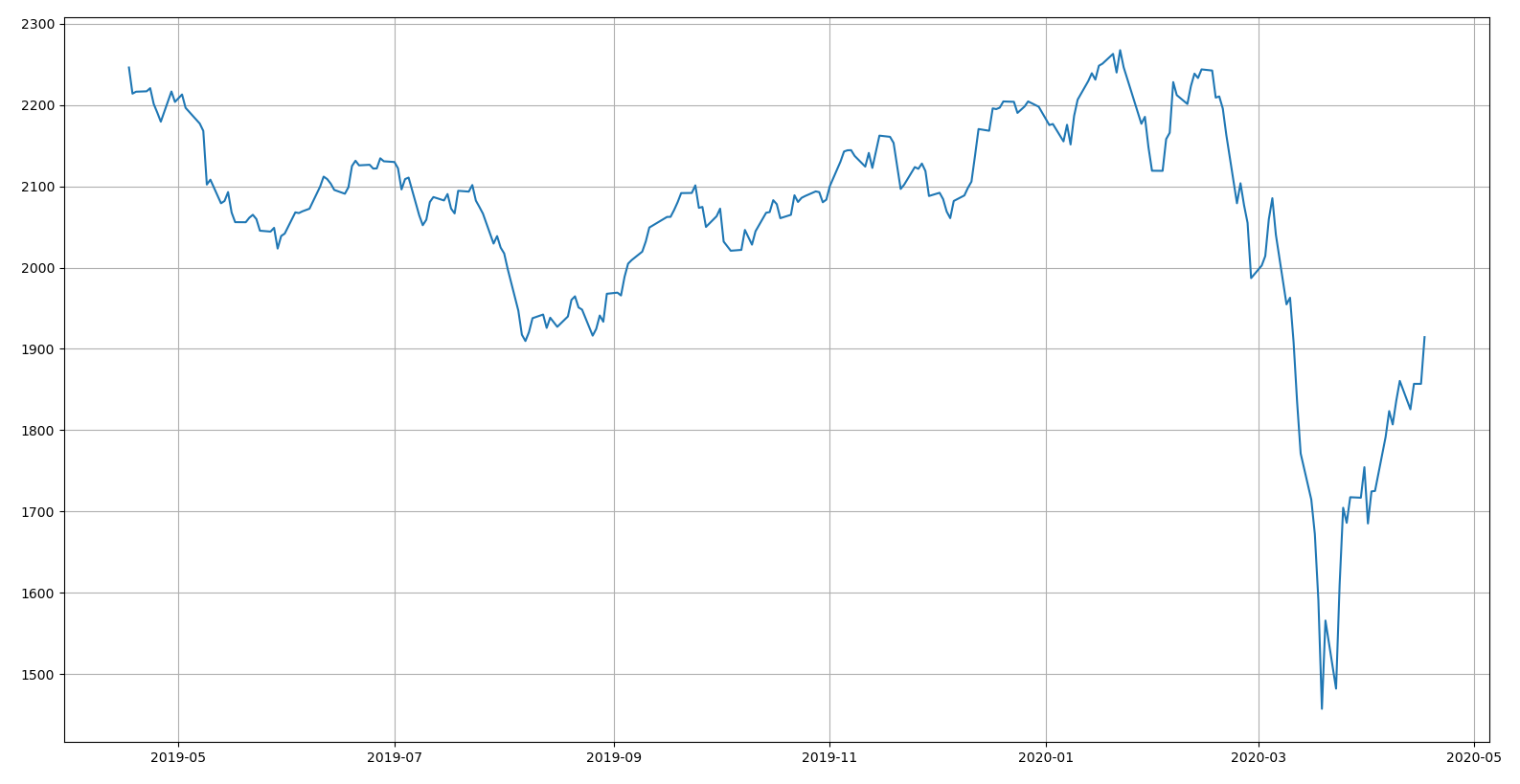
선형 회귀 학습
scikit-learn의 선형 회귀 알고리즘을 이용하여 학습을 진행한다.
미래의 결과를 예측할 수 있다면 좋겠지만, 신이 아닌 이상 미래를 예측하기는 힘들다.
그렇다면 10일 이전으로 돌아가서 현재를 예측해 보았을 때 현재의 값과 현재를 예측한 값이 얼마나 차이가 있는지 비교해보는 것은 의미가 있을 것 같다.
이러한 이유로 최근 10일을 제외한 데이터로 학습하고, 최근 10일의 데이터로 결과를 비교해 보고자 한다.
>>> from sklearn.linear_model import LinearRegression
>>> test_period = 10
>>> X_train = X[:-test_period]
>>> y_train = y[:-test_period]
>>> X_test = X[-test_period:]
>>> y_test = y[-test_period:]
>>> slr = LinearRegression()
>>> slr.fit(X_train, y_train)
>>> y_train_prediction = slr.predict(X_train)
>>> y_test_prediction = slr.predict(X_test)
선형 회귀 결과를 그래프로 시각화
학습 결과와 시험 결과를 그래프로 시각화 하면 다음 결과와 같다.
>>> plt.plot(dates[X].flatten(), y, '.-', label='trained KOSPI index')
>>> plt.plot(dates[X_test].flatten(), y_test, '.-', label='tested KOSPI index')
>>> plt.plot(dates[X_train].flatten(), y_train_prediction, c='limegreen', label='Linear Regression')
>>> X_last = X[-1:]
>>> y_last = y[-1:]
>>> y_last_prediction = slr.predict(X_last)
>>> plt.plot(dates[X_last].flatten(), y_last, 'rx', label='True Future')
>>> plt.plot(dates[X_last].flatten(), y_last_prediction, 'go', label='Model Prediction')
>>> plt.legend()
>>> plt.grid()
>>> plt.show()
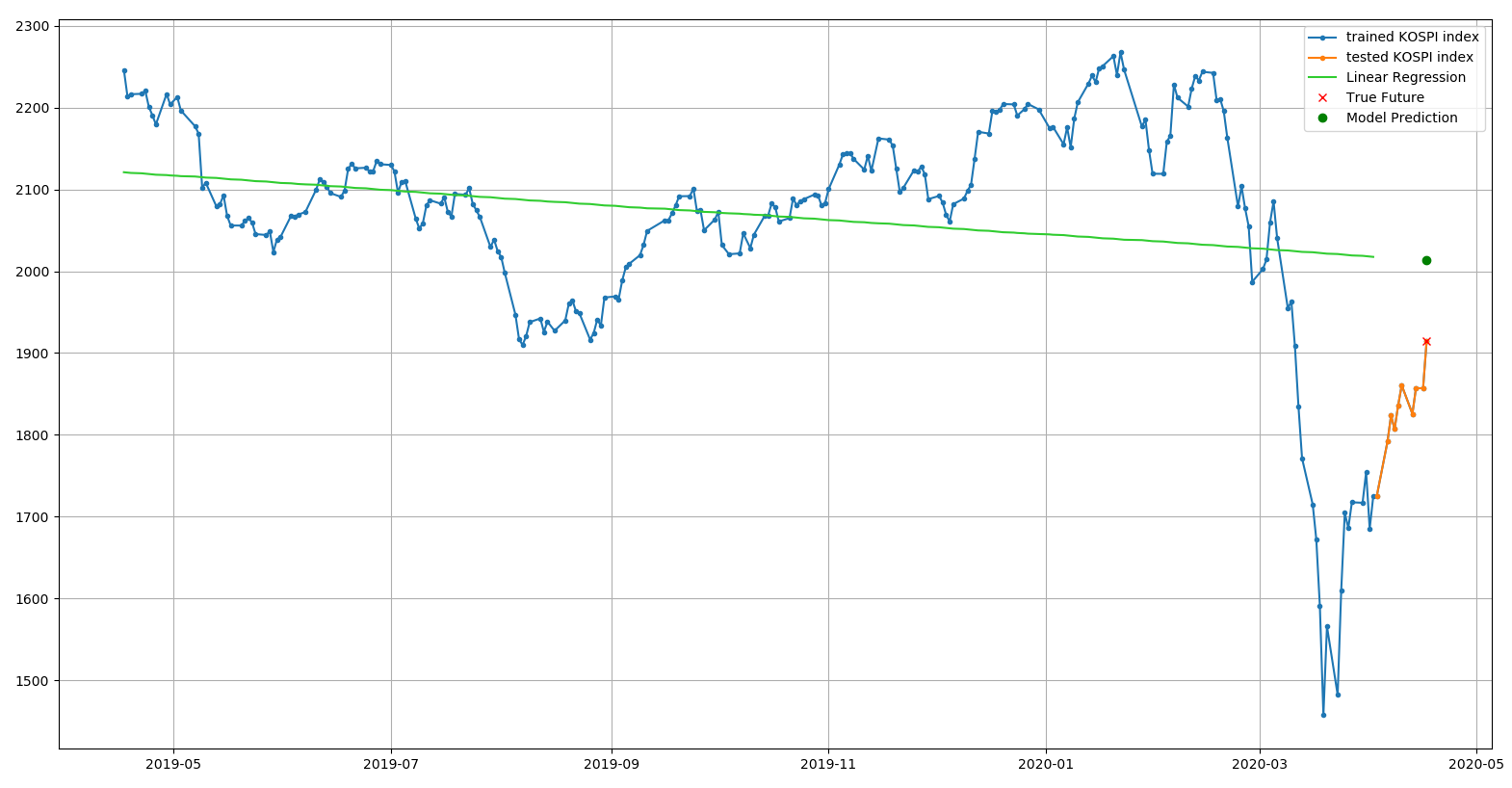
True Future로 표시된 지점이 현재의 값, Model Prediction으로 표시된 지점이 현재를 예측한 값이다.
예측한 값이 현재의 값과 정확히 일치하진 않지만 설정된 기간 동안의 방향성을 확인할 수 있고, 최근에 급락한 지수가 그 방향성을 향해 복귀하는 현상을 볼 수 있다.
선형 회귀 학습 모델 평가하기
학습 모델 성능 정량적으로 측정하는 방법 중의 하나는 Mean Absolute Error(MAE) 이다.
MAE 가 작을 수록 실제 샘플과의 차이가 작다는 의미인데, 학습 샘플의 MAE 는 94.451, 시험 샘플의 MAE 는 185.118 로 학습 데이터 샘플의 에러가 훨씬 적게 나타나고 있다. 이는 모델이 학습 데이터에 과대 적합되었다고 볼 수 있다.
>>> from sklearn.metrics import mean_squared_error, mean_absolute_error
>>> print('train MAE: %.3f, test MAE: %.3f' % (
>>> mean_absolute_error(y_train, y_train_prediction),
>>> mean_absolute_error(y_test, y_test_prediction)))
train MAE: 94.451, test MAE: 185.118
선형 회귀 모델을 다항 회귀로 변환
선형 회귀 모델을 $y = ax + b$ 의 1차식인 직선 그래프에서 $y = ax^2 + bx + c$ 와 같이 2차식인 곡선 그래프로 변환해보자.
이전과 코드는 동일하지만 훈련 데이터와 시험 데이터를 전처리하는 부분에 약간의 변경이 필요하다.
test_period = 10
>>> X_train = X[:-test_period]
>>> y_train = y[:-test_period]
>>> X_test = X[-test_period:]
>>> y_test = y[-test_period:]
위와 같이 훈련 데이터와 시험 데이터를 분리한 이후에, 2차 다항식을 사용하기 위해 scikit-learn의 PolynomialFeatures를 추가한다.
>>> from sklearn.preprocessing import PolynomialFeatures
>>> poly = PolynomialFeatures(degree=2)
>>> X_train_poly = poly.fit_transform(X_train)
>>> X_test_poly = poly.fit_transform(X_test)
다항 회귀로 변환된 데이터를 이용하여 기존과 동일한 방법으로 훈련한다.
>>> slr = LinearRegression()
>>> slr.fit(X_train_poly, y_train)
>>> y_train_prediction = slr.predict(X_train_poly)
>>> y_test_prediction = slr.predict(X_test_poly)
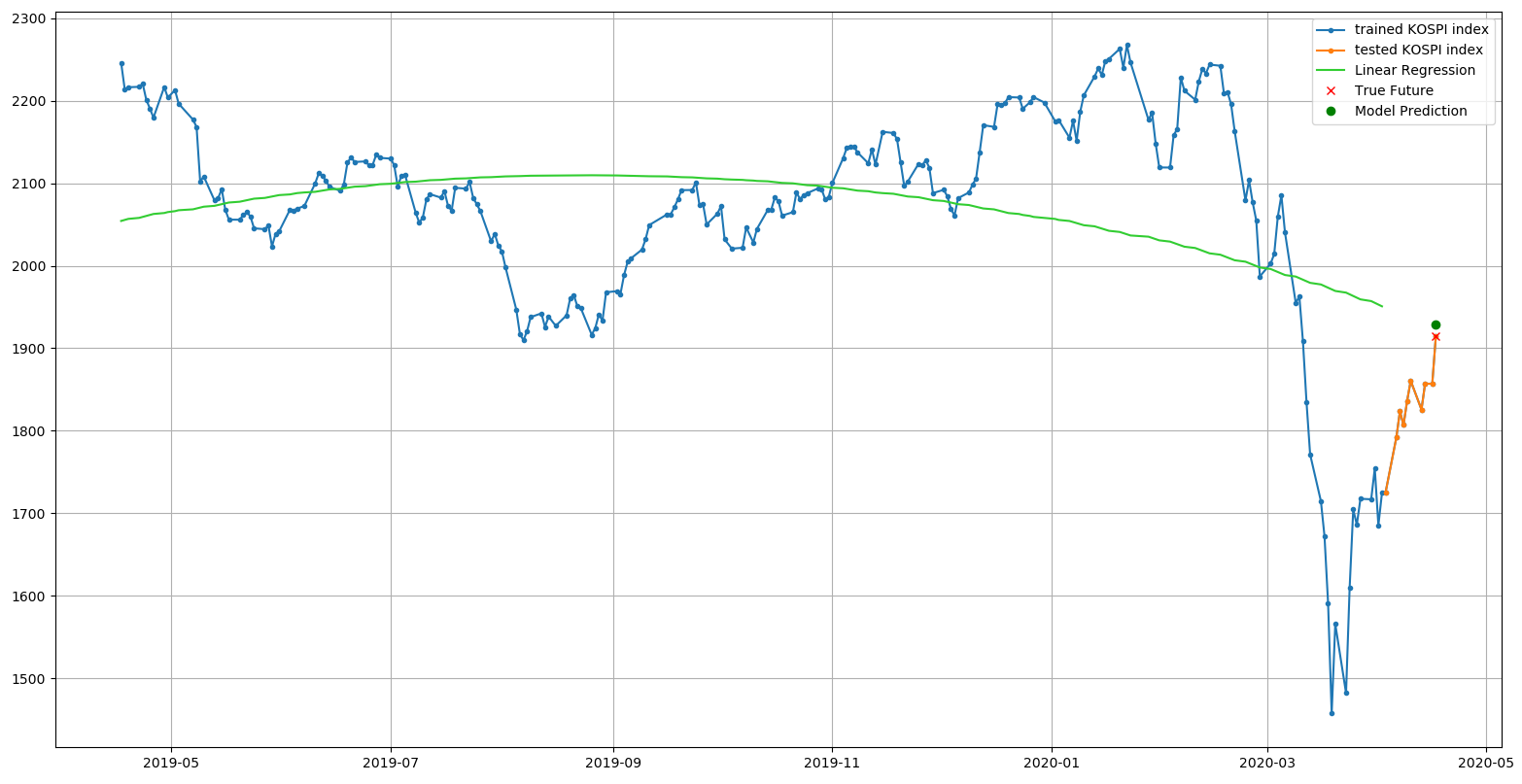
다항 회귀로 변환된 결과를 그래프로 시각화
>>> plt.plot(dates[X].flatten(), y, '.-', label='trained KOSPI index')
>>> plt.plot(dates[X_test].flatten(), y_test, '.-', label='tested KOSPI index')
>>> plt.plot(dates[X_train].flatten(), y_train_prediction, c='limegreen', label='Linear Regression')
>>> X_last = X[-1:]
>>> y_last = y[-1:]
>>> X_last_poly = poly.fit_transform(X_last)
>>> y_last_prediction = slr.predict(X_last_poly)
>>> plt.plot(dates[X_last].flatten(), y_last, 'rx', label='True Future')
>>> plt.plot(dates[X_last].flatten(), y_last_prediction, 'go', label='Model Prediction')
>>> plt.legend()
>>> plt.grid()
>>> plt.show()

1차식으로 표현된 그래프보다 2차식으로 표현된 그래프가 실제 결과에 더 근접하고 샘플 데이터와의 관계에서 오차가 적은 것으로 보인다.
다항 회귀 학습 모델 평가하기
선형 모델에 비해 다항 모델의 에러율이 얼마나 차이가 발생했는지 모델을 다시 평가해보자.
>>> from sklearn.metrics import mean_squared_error, mean_absolute_error
>>> print('train MAE: %.3f, test MAE: %.3f' % (
... mean_absolute_error(y_train, y_train_prediction),
... mean_absolute_error(y_test, y_test_prediction)))
train MAE: 95.678, test MAE: 108.888
이전 선형 모델의 시험 데이터 MAE 185.118 에서 다항 모델의 시험 데이터 MAE 는 108.888 로 에러율이 줄었고, 실제 데이터의 분포를 더 잘 반영하고 있는 것으로 보인다.
Written on April 18th, 2020 by Jonghyun Ho