Jonghyun Ho
LSTM 순환 신경망으로 코스피 지수 회귀 모델링

코스피 지수의 선형 회귀 분석 에서 코스피 지수의 이동 방향에 대해 확인할 수 있었다.
이번에는 딥러닝 순환 신경망 모델 중의 하나인 LSTM 을 이용하여 회귀 분석을 해보려고 한다.
Long Short-Term Memory (LSTM)
딥러닝 분야에서 시계열 데이터와 같은 시퀀스 데이터를 분석할 때에는 순환 신경망 (RNN, Recurrent Neural Network) 모델을 사용한다.
하지만 RNN 은 긴 시퀀스 데이터에 대한 학습이 어려운 단점이 있어, 이 단점을 보완한 LSTM (Long Short-Term Memory) 모델을 주로 사용한다.
참고 : LSTM
코스피 지수 읽기
딥러닝 학습을 위해 tensorflow 모듈도 함께 임포트 하였다.
>>> import numpy as np
>>> import pandas as pd
>>> import matplotlib.pyplot as plt
>>> import yfinance as yf
>>> import tensorflow as tf
학습 데이터를 충분히 확보하기 위해 20년의 긴 시간을 설정하였다.
>>> code = '^KS11' # KOSPI Composite Index
>>> kospi = yf.Ticker(code)
>>> kospi = kospi.history(period='20y')
>>> kospi = kospi[['Close']]
>>> print(kospi)
Close
Date
2000-04-21 767.16
2000-04-24 747.58
2000-04-25 737.20
2000-04-26 713.23
2000-04-27 692.07
... ...
2020-04-14 1857.08
2020-04-16 1857.07
2020-04-17 1914.53
2020-04-20 1898.36
2020-04-21 1879.38
[4922 rows x 1 columns]
데이터 전처리
X의 값은 날짜에 따른 순차적인 인덱스이고, y의 값은 각 날짜에 따른 코스피 지수의 종가를 가리킨다.
>>> dates = kospi.Close.index
>>> X = np.arange(len(dates)).reshape(-1, 1)
>>> y = kospi.Close.values
>>> y = y.reshape(-1, 1)
딥러닝 학습을 정상적으로 동작시키기 위해서는 데이터 정규화 과정이 필요하다.
>>> y_std = y.std()
>>> y_mean = y.mean()
>>> y = (y - y_mean) / y_std
현재를 기준으로 최근 10일 데이터는 시험에 사용하고, 그 외의 모든 이전 데이터들은 학습에 사용할 예정이다.
test_period = 10
X_train = X[:-test_period]
y_train = y[:-test_period]
X_test = X[-test_period:]
y_test = y[-test_period:]
학습이 진행되는 중에도 학습이 정상적으로 이루어지고 있는지 확인하기 위한 검증 데이터가 필요한데, scikit-learn을 사용하여 학습 데이터와 검증 데이터를 7 : 3 비율로 분배한다.
from sklearn.model_selection import train_test_split
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train, test_size=0.3, random_state=0)
tensorflow에 데이터를 전달하기 이전에 입력 형식을 맞추기 위해 2차원 데이터를 3차원 데이터로 변환한다.
X = X.reshape(-1, 1, 1)
X_train = X_train.reshape(-1, 1, 1)
X_val = X_val.reshape(-1, 1, 1)
X_test = X_test.reshape(-1, 1, 1)
LSTM 모델 생성
LSTM 레이어와, Dense 레이어를 쌓아 모델을 구성하였다.
>>> model = tf.keras.models.Sequential([
... tf.keras.layers.LSTM(8, input_shape=(None, 1)),
... tf.keras.layers.Dense(4),
... tf.keras.layers.Dense(1)])
>>> model.compile(optimizer='adam', loss='mse')
>>> print(model.summary())
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
lstm (LSTM) (None, 8) 320
_________________________________________________________________
dense (Dense) (None, 4) 36
_________________________________________________________________
dense_1 (Dense) (None, 1) 5
=================================================================
Total params: 361
Trainable params: 361
Non-trainable params: 0
_________________________________________________________________
None
데이터를 이용한 학습
각 훈련 회차마다 배치 데이터의 크기는 32 로 하고, 총 15 회 훈련을 할 수 있도록 설정하였다.
>>> hist = model.fit(X_train, y_train, epochs=15, batch_size=32, validation_data=(X_val, y_val))
Epoch 1/15
108/108 [==============================] - 0s 3ms/step - loss: 1.0477 - val_loss: 0.9480
Epoch 2/15
108/108 [==============================] - 0s 1ms/step - loss: 0.8357 - val_loss: 0.5738
Epoch 3/15
108/108 [==============================] - 0s 1ms/step - loss: 0.4066 - val_loss: 0.2169
Epoch 4/15
108/108 [==============================] - 0s 1ms/step - loss: 0.2040 - val_loss: 0.2224
Epoch 5/15
108/108 [==============================] - 0s 1ms/step - loss: 0.2585 - val_loss: 0.1845
Epoch 6/15
108/108 [==============================] - 0s 1ms/step - loss: 0.1608 - val_loss: 0.0946
Epoch 7/15
108/108 [==============================] - 0s 1ms/step - loss: 0.1267 - val_loss: 0.0934
Epoch 8/15
108/108 [==============================] - 0s 1ms/step - loss: 0.1159 - val_loss: 0.1469
Epoch 9/15
108/108 [==============================] - 0s 1ms/step - loss: 0.1225 - val_loss: 0.0966
Epoch 10/15
108/108 [==============================] - 0s 1ms/step - loss: 0.1187 - val_loss: 0.0895
Epoch 11/15
108/108 [==============================] - 0s 1ms/step - loss: 0.1185 - val_loss: 0.1708
Epoch 12/15
108/108 [==============================] - 0s 1ms/step - loss: 0.1074 - val_loss: 0.0947
Epoch 13/15
108/108 [==============================] - 0s 1ms/step - loss: 0.1116 - val_loss: 0.0906
Epoch 14/15
108/108 [==============================] - 0s 1ms/step - loss: 0.1234 - val_loss: 0.1260
Epoch 15/15
108/108 [==============================] - 0s 1ms/step - loss: 0.1241 - val_loss: 0.1034
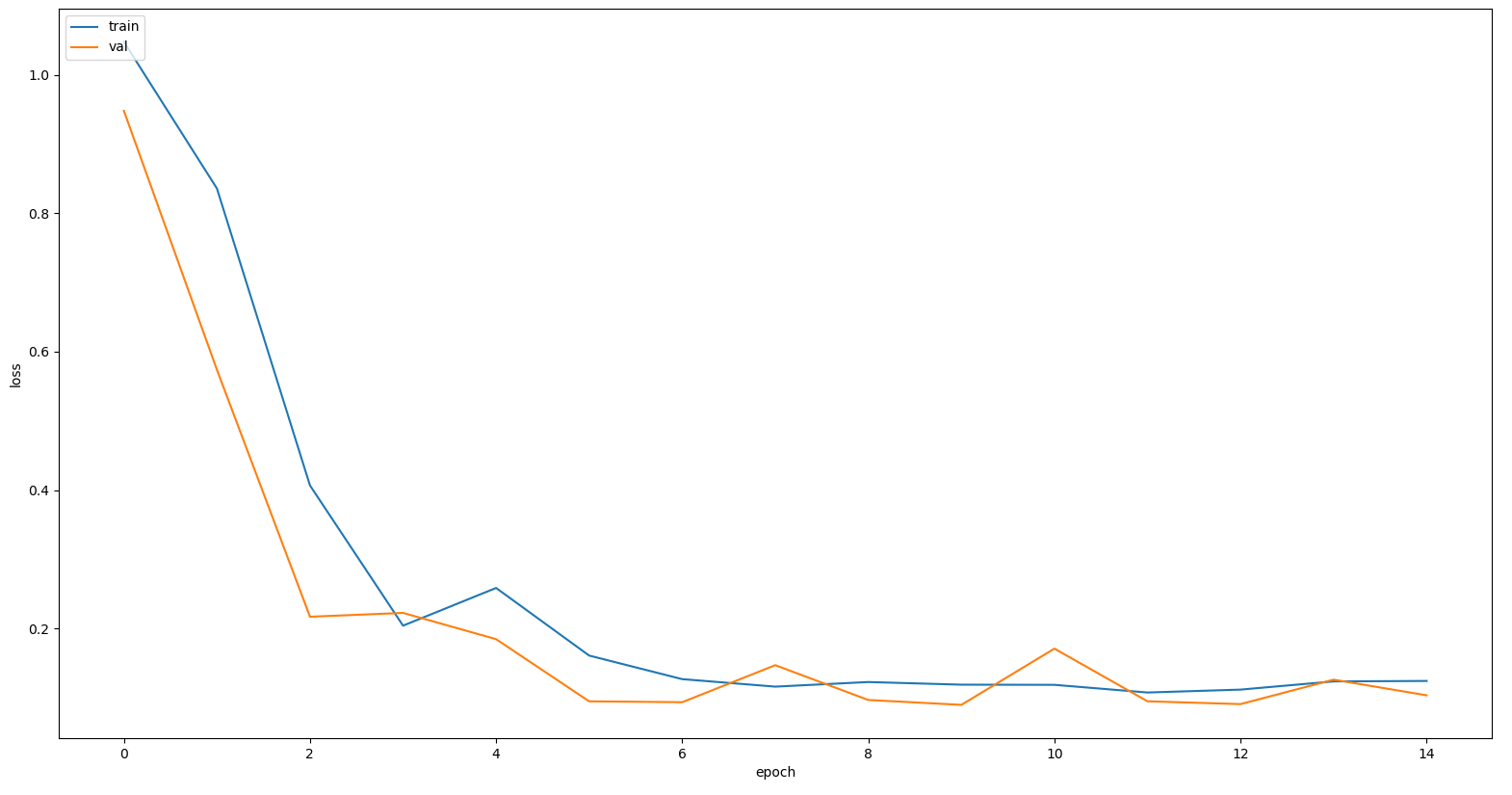
훈련 데이터와 검증 데이터의 Mean Squared Error (MSE) 손실 함수의 결과 값은 훈련이 진행되면서 유사하게 수렴하며 줄어드는 것을 확인할 수 있다.
>>> plt.plot(hist.history['loss'])
>>> plt.plot(hist.history['val_loss'])
>>> plt.ylabel('loss')
>>> plt.xlabel('epoch')
>>> plt.legend(['train', 'val'], loc='upper left')
>>> plt.show()
>>> trainScore = model.evaluate(X_train, y_train, verbose=0)
>>> valScore = model.evaluate(X_val, y_val, verbose=0)
>>> testScore = model.evaluate(X_test, y_test, verbose=0)
>>> print('Train Score: ', trainScore)
>>> print('Validataion Score: ', valScore)
>>> print('Test Score: ', testScore)
Train Score: 0.11737338453531265
Validataion Score: 0.10335058718919754
Test Score: 0.18995893001556396
학습 결과를 그래프로 시각화
20년의 기간동안 코스피 지수를 학습한 결과를 그래프로 시각화 하면 다음과 같다.
get_dates 함수는 이전에 만들었던 인덱스를 통해 날짜를 얻어오기 위해 사용하고, denorm 함수는 정규화된 데이터를 복원하기 위해 사용하였다.
>>> def get_dates(x):
... return dates[x].flatten()
>>> def denorm(y):
... return y * y_std + y_mean
>>> prediction = model.predict(X.reshape(-1, 1, 1), batch_size=32)
>>> plt.plot(get_dates(X[:-10]), denorm(y[:-10]), label='trained KOSPI index')
>>> plt.plot(get_dates(X_test), denorm(y_test), '.-', label='tested KOSPI index')
>>> plt.plot(get_dates(X), denorm(prediction), c='limegreen', label='LSTM')
>>> X_last = X[-1:]
>>> y_last = y[-1:]
>>> y_last_prediction = model.predict(X_last.reshape(-1, 1, 1))
>>> plt.plot(get_dates(X_last), denorm(y_last), 'rx', label='True Future')
>>> plt.plot(get_dates(X_last), denorm(y_last_prediction), 'go', label='Model Prediction')
>>> plt.legend()
>>> plt.grid()
>>> plt.show()

2019년 초 이후의 데이터만 축소하여 보면 다음과 같다.
base_index = np.where(dates == pd.Timestamp(2019, 1, 2))
base_index = base_index[0].tolist()[0]
plt.plot(get_dates(X[base_index:-10]), denorm(y[base_index:-10]), label='trained KOSPI index')
plt.plot(get_dates(X_test), denorm(y_test), '.-', label='tested KOSPI index')
plt.plot(get_dates(X[base_index:]), prediction[base_index:] * y_std + y_mean, c='limegreen', label='LSTM')
plt.plot(get_dates(X_last), denorm(y_last), 'rx', label='True Future')
plt.plot(get_dates(X_last), denorm(y_last_prediction), 'go', label='Model Prediction')
plt.legend()
plt.grid()
plt.show()
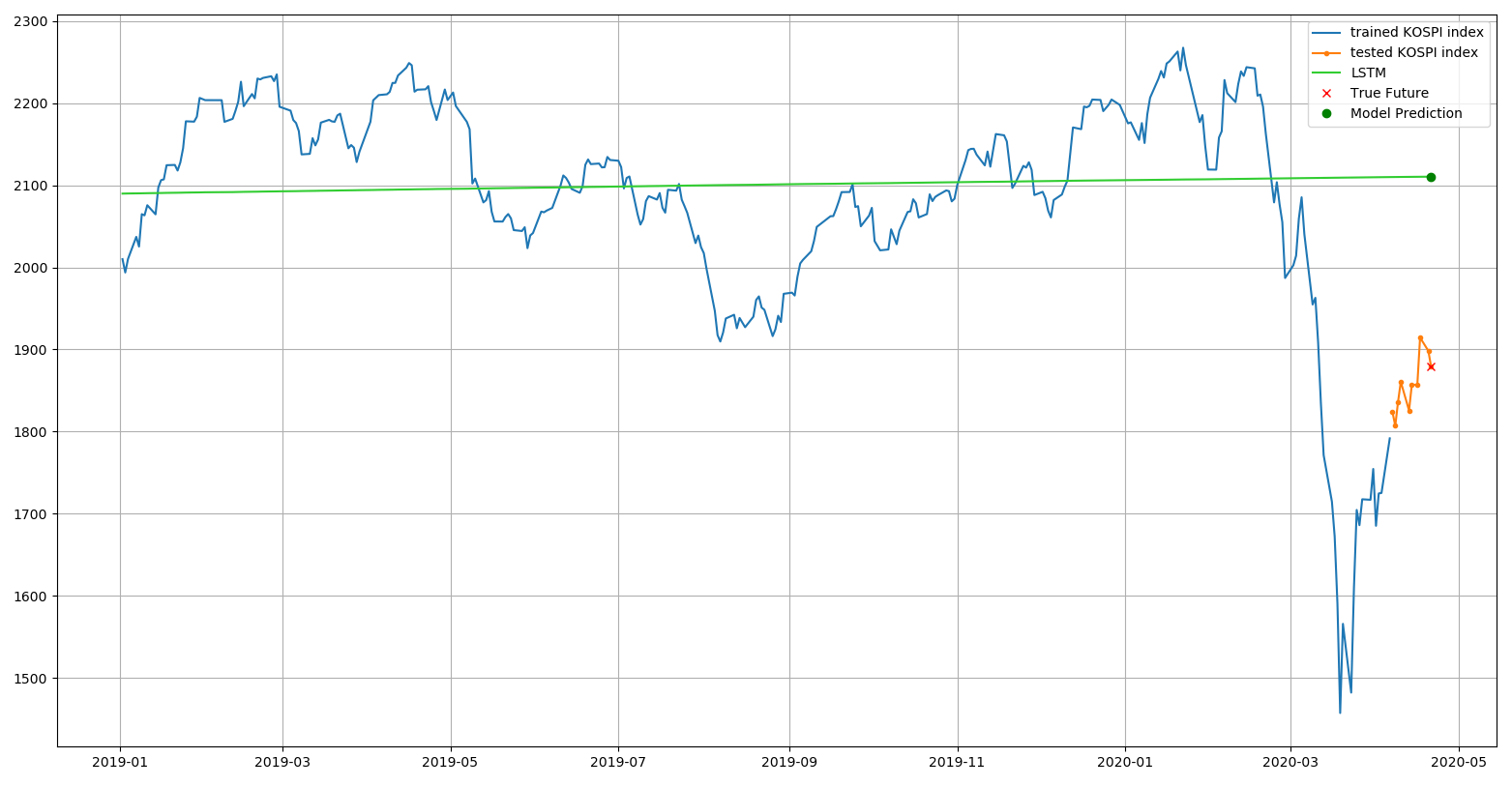
코스피 지수의 선형 회귀 분석 에서도 머신 러닝을 이용한 회귀 분석을 하였지만 어떻게 입력 데이터를 설정했는지, 적용한 알고리즘이 무엇인지에 따라 다른 결과를 확인할 수 있었다.
어느 것이 정답이라고 분명히 이야기할 수는 없는 분야이고 이 그래프가 현실 세계를 제대로 반영하고 있는지는 알 수 없지만, 딥러닝을 적용하였을 때 각 모델의 레이어에서 사용되는 매개변수의 수가 많고 다양한 점을 미루어보아 지수의 움직임을 좀 더 정확히 반영한 것이 아닐까 생각된다.
Written on April 22nd , 2020 by Jonghyun Ho